Poisson–Boltzmann equation

The Poisson–Boltzmann equation is a differential equation that describes electrostatic interactions between molecules in ionic solutions. It is the mathematical base for the Gouy–Chapman double layer (interfacial) theory; first proposed by Gouy in 1910 and complemented by Chapman in 1913. The equation is important in the fields of molecular dynamics and biophysics because it can be used in modeling implicit solvation, an approximation of the effects of solvent on the structures and interactions of proteins, DNA, RNA, and other molecules in solutions of different ionic strength. It is often difficult to solve the Poisson–Boltzmann equation for complex systems, but several computer programs have been created to solve it numerically.

The equation can be written as (in cgs):

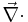\vec{\nabla}\cdot\left[\epsilon(\vec{r})\vec{\nabla}\Psi(\vec{r})\right] = -4\pi\rho^{f}(\vec{r}) - 4\pi\sum_{i}c_{i}^{\infty}z_{i} q \lambda(\vec{r}) \exp \left[{\frac{-z_{i}q\Psi(\vec{r})}{k_B T}}\right]

or (in SI units or mks):

\vec{\nabla}\cdot\left[\epsilon(\vec{r})\vec{\nabla}\Psi(\vec{r})\right] = -\rho^{f}(\vec{r}) - \sum_{i}c_{i}^{\infty}z_{i} q \lambda(\vec{r}) \exp \left[{\frac{-z_{i}q\Psi(\vec{r})}{k_B T}}\right]

where \vec{\nabla}\cdot is the divergence operator, 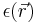\epsilon(\vec{r}) represents the position-dependent dielectric, 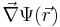\vec{\nabla} \Psi(\vec{r}) represents the gradient of the electrostatic potential, 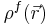\rho^{f}(\vec{r}) represents the charge density of the solute, 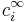c_{i}^{\infty} represents the concentration of the ion i at a distance of infinity from the solute, 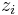z_{i} is the charge of the ion, q is the charge of a proton, 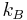k_B is the Boltzmann constant, T is the temperature, and 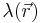\lambda(\vec{r}) is a factor for the position-dependent accessibility of position r to the ions in solution. If the potential is not large compared to kT, the equation can be linearized to be solved more efficiently, leading to the Debye–Hückel equation.[1][2][3]

See also

References

  1. ^ Fogolari F, Brigo A, Molinari H. (2002). The Poisson–Boltzmann equation for biomolecular electrostatics: a tool for structural biology. J Mol Recognit 15(6):377–392. (See this paper for derivation.)
  2. ^ G.L. Gouy, j. de phys 9, 457 (1910)
  3. ^ D.L. Chapman, Philos. Mag. 25, 475 (1913)

External links